Maitriser les pertes de charge linéaires dans les conduites
La maîtrise des pertes de charge dans les circuit hydraulique est un défi majeur en mécanique des fluides. Ces pertes, représentées par le terme ΔH dans l’équation de Bernoulli, peuvent avoir des conséquences importantes sur le fonctionnement des systèmes hydrauliques. Elles peuvent être dues aux frottements sur les parois des conduites, à la turbulence de l’écoulement ou à des singularités.
Comprendre les pertes de charge linéaires est essentiel pour concevoir des systèmes hydrauliques efficaces et fiables. Cet article vous guide à travers les principales notions théoriques et les équations empiriques permettant d’évaluer ces pertes de charge.
1- Expression générale des pertes de charge linéaires
Lorsqu’un fluide s’écoule dans une conduite cylindrique, la différence de charge ΔH entre deux sections distantes de L dépend de plusieurs paramètres :
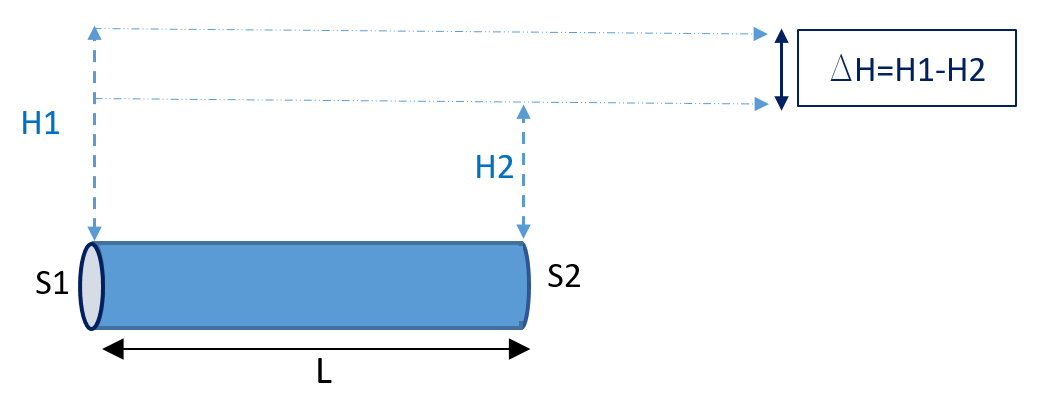
- La nature du fluide, caractérisée par sa masse volumique ρ et sa viscosité dynamique μ
- La vitesse moyenne du fluide V (ou le débit Q et la section S)
- Le diamètre de la conduite D
- La rugosité des parois, caractérisée par la hauteur moyenne des aspérités ε et leur espacement e
En appliquant l’analyse dimensionnelle, on montre que cette équation peut se ramener à une fonction de 6 paramètres adimensionnels :
$\Delta H = f\left(\frac{L}{D}, \frac{\rho VD}{\mu}, \frac{\epsilon}{D}\right)$
Le nombre de Reynolds $Re = \frac{\rho VD}{\mu}$ représente le rapport entre les forces d’inertie et les forces de cisaillement dues à la viscosité. Il permet de caractériser le régime d’écoulement, laminaire ou turbulent.
- Les écoulements laminaires: $Re<2400$
- Les écoulements turbulents: $Re>4000$
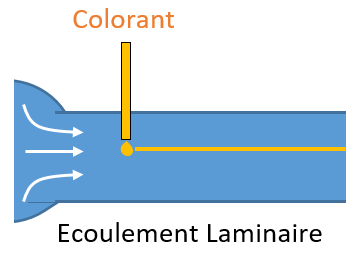
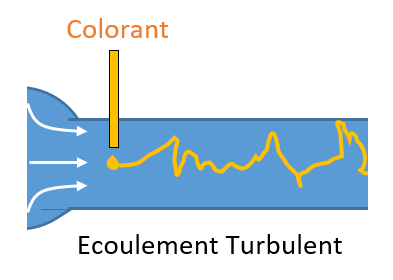
Le rapport $\frac{\epsilon}{D}$, quant à lui, caractérise la rugosité relative de la conduite. Plus ce rapport est grand, plus les aspérités de la paroi influencent l’écoulement.
Le tableau ci-après donne des valeurs de ε pour des conduites à l’état neuf.
| Matériau | Condition | Rugosité absolue en mm ε (0) | ||
|---|---|---|---|---|
| Acier | Feuille de métal | 0.05 | ||
| Acier inoxydable | 0.002 | |||
| Commercial | 0.046 | |||
| Rivé | 3 | |||
| Rouillé | 2 | |||
| Fer | Fonte | 0.26 | ||
| Forgé | 0.046 | |||
| Galvanisé | 0.15 | |||
| Fonte asphaltée | 0.12 | |||
| Cuivre | Tube étiré | 0.002 | ||
| Plastique | Tube étiré | 0.0015 | ||
| Béton | Lisse | 0.04 | ||
| Caoutchouc | Lisse | 0.012 | ||
| Bois | Défoncé | 0.5 |
A noter que la rugosité ε augmente en utilisant la conduite, elle est supposée varier linéairement dans le temps suivant la relation : ε(t)= ε(0) +αt
Où ε(t) est ma rugosité absolue qui correspond à l’âge t en année
α coefficient de l’âge qui dépend du matériau de la conduite, du revêtement ,de l’hydraulique de l’écoulement et surtout la physico-chimie du liquide. Le tableau suivant donne les valeurs de α pour l’eau.
| Caractéristiques de l’eau | Coefficient α | |||
|---|---|---|---|---|
| Minimale | Moyenne | Maximale | ||
| Eau peu minéralisée, non agressive, contenance en fer et en matière organique très faible (eau de haute montagne) | 0.005 | 0.025 | 0.055 | |
| Eau peu minéralisée, mais corrosive (pH faible), contenance en fer et en matière organique ne dépassent pas 3mg/l | 0.055 | 0.07 | 0.18 | |
| Eau très corrosive(pH très faible), mais contenant moins de 150 mg/l de chlorures de sulfates, contenance en fer supérieure à 3mg/l (eau de fleuve) | 0.18 | 0.2 | 0.4 | |
| Eau corrosive, contenant 500 à 700 mg/l de chlorure et sulfates, contenance en matière organique très grande (eau de grand fleuve) | 0.4 | 0.51 | 0.6 | |
| Eau très minéralisé de grand dureté, pH supérieur à 7, résidu solide supérieur à 2000mg/l | 0.6 | 0.7 | 1 | |
2- Détermination expérimentale du coefficient de perte de charge
Les travaux de Nikuradse, dans les années 1930, ont permis de déterminer expérimentalement le coefficient de perte de charge linéaire λ en fonction de Re et ε/D. Ses résultats ont été synthétisés dans le diagramme de Nikuradse, qui reste une référence encore aujourd’hui.
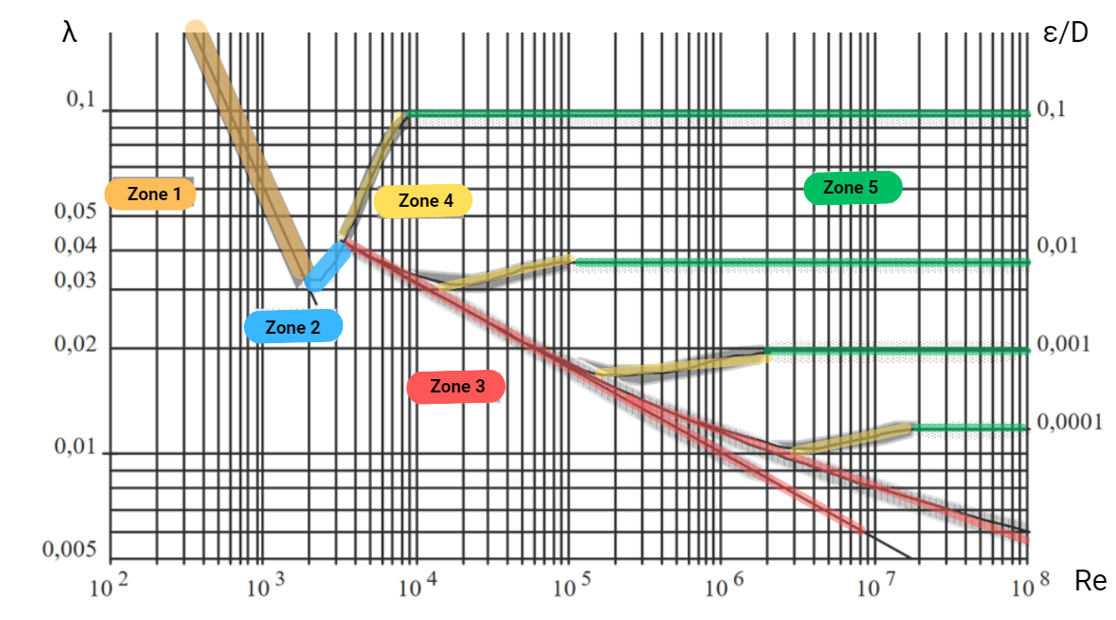
Ce diagramme fait apparaître 5 zones distinctes, selon le régime d’écoulement et la rugosité relative :
- Zone 1 et 2 (écoulement lisse ou laminaire) :
– λ ne dépend que de Re
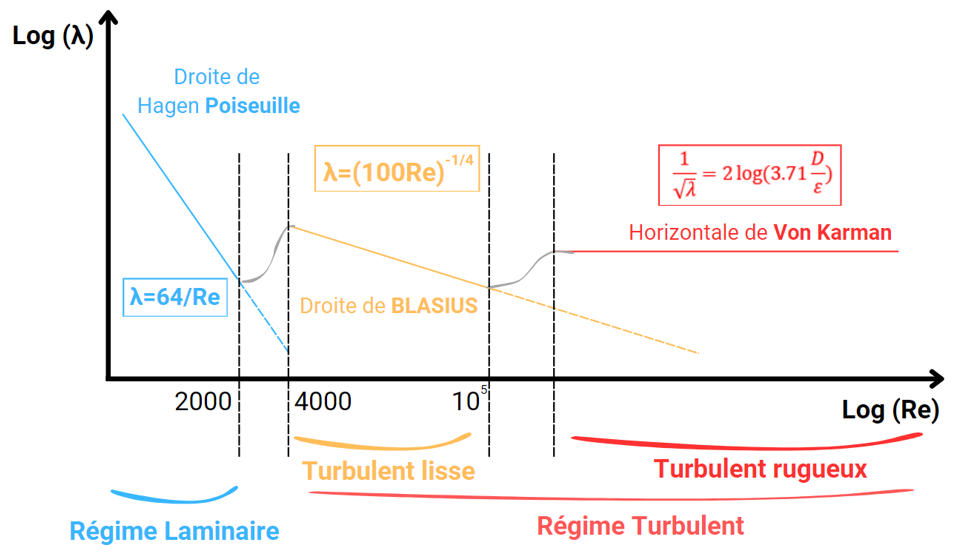
– Loi de Hagen Poiseuille (valable pour Re<2000)
$\boxed{\lambda = \frac{64}{\text{Re}}}$
- Zone 3 (écoulement turbulent lisse) :
– λ ne dépend que de Re
– deux formules ont été proposées :
La formule de Blasius (valable uniquement pour Re<105)
$\boxed{\lambda = \frac{0.316}{\text{Re}^{1/4}} = \left(100 \, \text{Re}\right)^{-1/4}}$
La 1ère formule de Von Karman (pour Re>105)
$\boxed{\frac{1}{\sqrt{\lambda}} = 2 \log\left(\text{Re} \sqrt{\lambda} – 0.8\right) = 2 \log\left(\frac{\text{Re} \sqrt{\lambda}}{2.51}\right)
}$
- Zone 4 (écoulement semi-rugueux) :
– λ dépend de Re et ε/D
- Zone 5 (écoulement rugueux) :
– λ ne dépend que de ε/D
– 2ème formule de Von Karman:
$\boxed{\frac{1}{\sqrt{\lambda}} = 2 \log\left(\frac{D}{\epsilon} + 1.14\right) = 2 \log\left(\frac{3.71 \, D}{\epsilon}\right)
}$
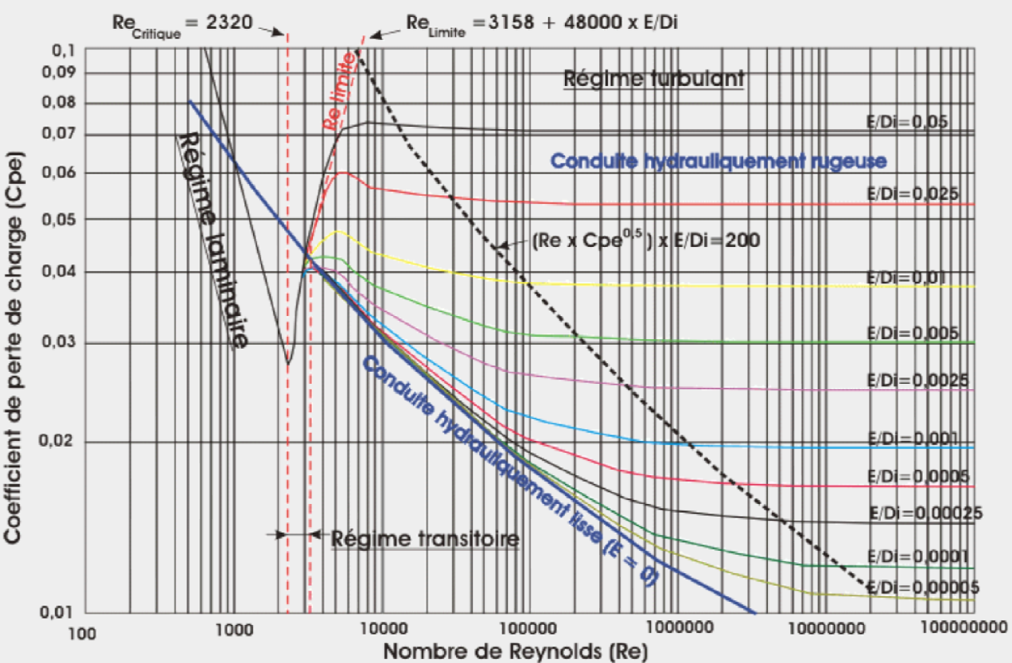
Contrairement aux conduites de Nikuradse dont les aspérités étaient homogènes, les aspérités des conduites réelles sont hétérogènes dans leurs tailles et leur espacement. Les expériences menées à partir des conduites réelles ont abouti à un schéma assez semblable à celui de Nikuradse.
L’ensemble des résultats peut être reporté sur un graphique appelé diagramme de Moody qui n’est que la représentation de la formule empirique de Colebrook :
$\boxed{\frac{1}{\sqrt{\lambda}} = 2 \log\left(\frac{\text{Re} \sqrt{\lambda}}{2.51} + \frac{3.71 \, D}{\epsilon}\right)}
$
Bien que cette équation soit implicite, elle permet de prendre en compte à la fois la rugosité et le régime d’écoulement. Des abaques et tableaux en facilitent l’utilisation pratique.
3- Formules empiriques pour les pertes de charge linéaires
En complément du diagramme de Moody, de nombreuses formules empiriques ont été développées pour estimer les pertes de charge linéaires, notamment pour des géométries de conduites non circulaires.
Parmi les plus utilisées :
- Formule de Chezy : $\boxed{V = C \sqrt{R_H j}}$
avec C le coefficient de Chezy dépendant de la nature des parois (100 pour la fonte lisse, 40 pour les conduites rugeuses)
Il convient de définir le nombre de Reynolds de l’écoulement:
$\boxed{R_H = \frac{S}{P} = \frac{D_H}{4}}$
avec S la section de la conduite, P le périmètre de la conduite, $D_H$ le diamètre hydraulique Formule de Lechapt et Calmont :
$\boxed{j = 0,0011 \cdot Q^{1,89} \cdot D^{-5,01}}$
avec Q le débite de l’écoulement et D le diamètre de la conduite (Formule pratique pour de l’eau et une rugosité équivalente de 10⁻⁴ m)- Formule de Manning-Strickler :
$\boxed{V = \left(K R_H\right)^{2/3} \cdot j^{1/2}}$avec K=1/n, K coefficient de Strikler et n coefficient de Manning (Cette formule est principalement utilisé pour les gros diamètres)
Formule de Hazen-Williams :
$\boxed{j = 6{,}84 \left(\frac{V}{C_{HW}}\right)^{1{,}85} D^{-1{,}17}}$
avec $C_HW$ étant le coefficient de Hazen-Williams dépendant de la nature des parois ,V la vitesse d’écoulement et D diamètre de la conduite
Le choix de la formule dépend du type d’application, des données disponibles et du niveau de précision requis. Certaines formulations plus simples peuvent être utilisées lorsque les pertes singulières sont négligeables.
Conclusion
La compréhension et la maîtrise des pertes de charge linéaires dans les conduites sont essentielles pour concevoir des systèmes hydrauliques performants. Les outils théoriques et empiriques présentés dans cet article permettent d’estimer ces pertes avec précision, en tenant compte des caractéristiques du fluide, de la géométrie et de l’état de la conduite.
Grâce à cette connaissance approfondie, les ingénieurs peuvent optimiser le dimensionnement des réseaux de transport de fluides, qu’il s’agisse d’eau, de pétrole, de gaz ou d’autres applications industrielles. Cela contribue à améliorer l’efficacité énergétique, la fiabilité et la durabilité de ces systèmes.