LOGO du site

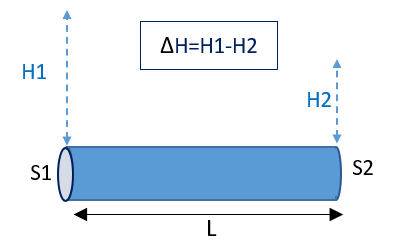
PERTE DE CHARGE: Définition, calcul et types
(linéaires et singulières)

Pertes de charges et pression à cause des singularités

La maîtrise du calcul de la perte de charge est essentielle pour garantir l’efficacité énergétique, la sécurité et la performance des installations hydrauliques. Elle permet d’anticiper les besoins en puissance, d’éviter les dysfonctionnements et de réduire les coûts d’exploitation. La compréhension et la quantification des pertes de charge est donc indispensable dans le domaine de l’ingénierie des fluides.

1- Définition de la perte de charge (PDC)

La perte de charge est un concept fondamental en mécanique des fluides, désignant la diminution de pression d’un fluide en mouvement dans un système. Ce phénomène, est due principalement aux :

  • Frottements du fluide contre la paroi du système,
  • Obstacles rencontrés toute au long le parcours du système.

Cette grandeur joue un rôle crucial dans la conception et l’optimisation des systèmes et circuits hydrauliques.

Les pertes de charge sont exprimées en mètre (m), symbolisée par ΔH.

2- Quelle est la différence entre les pertes de charges linéaires et le pertes de charge singulières ?

Pertes de charges linéaires

Les pertes de charge linéaires, aussi appelées régulières, se produisent tout au long des sections droites des conduites. Elles résultent de la friction entre le fluide et les parois internes du tuyau. Ces pertes sont directement proportionnelles à la longueur de la conduite et dépendent de facteurs tels que la rugosité des parois, la viscosité du fluide, et la vitesse d’écoulement.

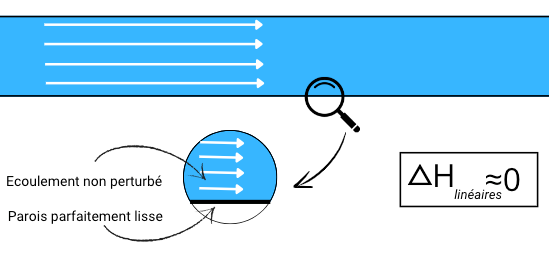
écoulement dans une conduite parfaitement lisse
Ecoulement dans une conduite parfaitement lisse
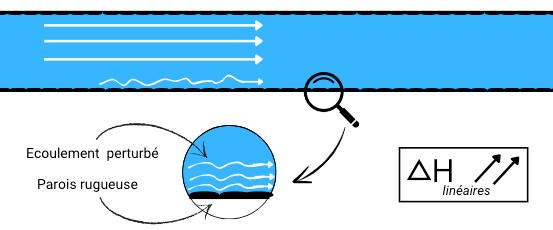
écoulement dans une conduite rugueuse
Ecoulement dans une conduite rugueuse
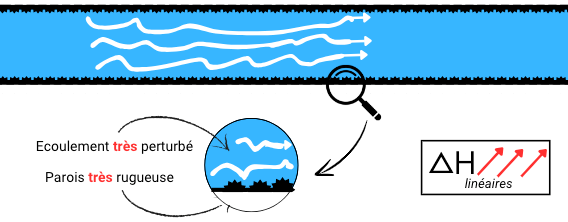
écoulement dans une conduite très rugueuse
Ecoulement dans une conduite très rugueuse

Les pertes de charges linéaires se calcule par la formule suivante :

$$\boxed{\Delta H_{Lineaires} = \lambda \cdot \frac{L}{2g} \cdot \frac{V^2}{D}}$$

Où :

  • $\Delta H_{Lineaires}$ : Pertes de charges linéaires (m),
  • $\lambda$: Coefficient de perte de charge (sans unité),
  • $L$ : Longueur de la conduite (m),
  • $g$ : Accélération de pesanteur (m/s²) ,
  • $D$ : Diamètre de la conduite (m),
  • $V$ : Vitesse de l’écoulement (m/s).

Pertes de charges singulières

Les pertes de charge singulières, ou locales, surviennent à des points spécifiques du système où l’écoulement subit des perturbations importantes. Elles sont causées par des changements brusques dans la géométrie ou la direction de l’écoulement, comme les coudes, les vannes, les élargissements ou rétrécissements soudains. Contrairement aux pertes linéaires, elles sont indépendantes de la longueur du tuyau et sont généralement calculées à l’aide de coefficients de perte de charge spécifiques.

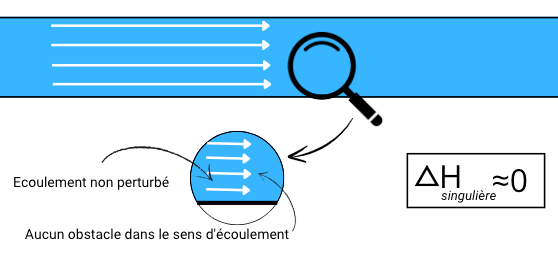
écoulement sans pertes de charge singulières
Ecoulement sans pertes de charge singulières
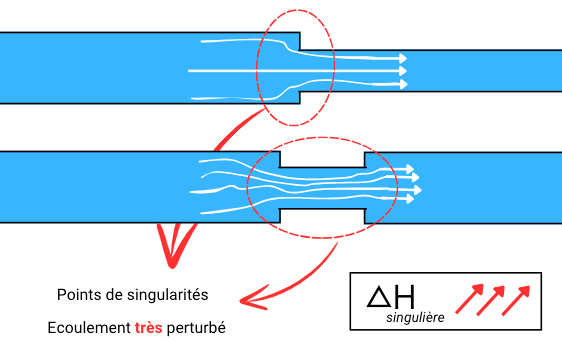
écoulement avec pertes de charge singulières (changement de section)
Ecoulement avec pertes de charge singulières (changement de section)

Les pertes de charges singulières se calcule par la formule suivante :

$$\boxed{\Delta H_{Singulière} = k \cdot \frac{V^2}{2g}}$$

Où :

  • $\Delta H_{Singulière}$: Pertes de charges singulière (m),
  • $k$: Coefficient de perte de charge singulière (sans dimension),
  • $g$ : Accélération de pesanteur (m/s²) ,
  • $V$ : Vitesse moyenne de l’écoulement (m/s).

Pertes de charges totales

Dans la pratique, la perte de charge totale d’un système est la somme de ces deux types de pertes. Bien que les pertes linéaires soient souvent prédominantes dans les longues conduites droites, les pertes singulières peuvent devenir significatives, voire dominantes, dans les systèmes complexes comportant de nombreux raccords et accessoires.

$$\boxed{\Delta H_{Total} = \Delta H_{Linéaires} + \Delta H_{Singulières}}$$

Où : 

  • $\Delta H_{Total}$: Pertes de charges totales (m),
  • $\Delta H_{Linéaires}$: Pertes de charges linéaires (m),
  • $\Delta H_{Singulières}$: Pertes de charges singulières (m).

La distinction entre ces deux types de pertes est essentielle pour une conception précise et une gestion efficace des systèmes hydrauliques, permettant d’optimiser les performances et de réduire les coûts énergétiques.

3- Exemple de calcul des pertes de charges dans un circuit

On considère un système hydraulique composé d’un réservoir et d’une conduite avec plusieurs sections, la conduite est dotée d’une vanne (K1) et un clapet (K2) comme illustré sur la figure. Le système présente les caractéristiques suivantes :

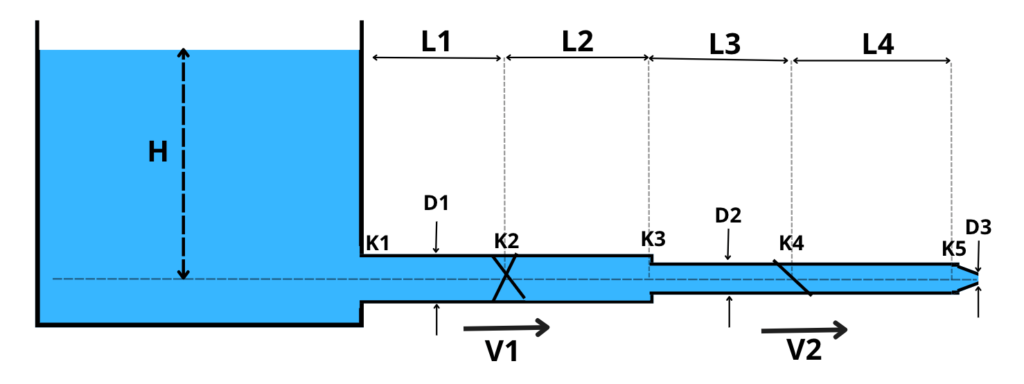
schéma d'un réservoir lié à une conduite
  • Accélération de la pesanteur : g = 9,81 m/s²
  • Réservoir d’une hauteur H=20 m

1er tronçon : 

1ere partie :

  • Longueur L1= 8m,
  • Diamètre D1= 200mm,
  • Vitesses de l’écoulement V1= 0.69 m/s
  • Singularités : Sotie du réservoir K1=0,5 ,Vanne K2=0,2
  • Coefficient de perte de charge linéaire λ1=0,01

2éme partie :

  • Longueur L2= 4m,
  • Diamètre D1= 200mm,
  • Vitesses de l’écoulement V1= 0.69 m/s
  • Singularité : Changement de section K3= 0,35
  • Coefficient de perte de charge linéaire λ1=0,01

2éme tronçon :

1ere partie :

  • Longueur L3= 4m,
  • Diamètre D2= 100mm,
  • Vitesses de l’écoulement V2= 2,78 m/s
  • Singularités : Clapet K4=0,3
  • Coefficient de perte de charge linéaire λ2=0,02

2éme partie :

  • Longueur L4= 6m,
  • Diamètre D2= 100mm, D3=50mm
  • Vitesses de l’écoulement V2= 2,78 m/s, V3 (à la sorite)= 11,13m/s
  • Singularité : Rétrécissement K5 = 0,1
  • Coefficient de perte de charge linéaire λ2=0,02

Résultats

  1. Calcul des pertes de charge linéaires :
    • 1er tronçon :

$\Delta H_{L1} = 0,01 \times \frac{8}{0,2} \times \frac{0,69^2}{2 \times 9,81} = 0,0096 \text{ m}$

$\Delta H_{L2} = 0,01 \times \frac{4}{0,2} \times \frac{0,69^2}{2 \times 9,81} = 0,0048 \text{ m} $

  • 2eme tronçon :

$\Delta H_{L3} = 0,02 \times \frac{4}{0,1} \times \frac{2,78^2}{2 \times 9,81} = 0,3156 \text{ m} $

$\Delta H_{L4} = 0,02 \times \frac{6}{0,1} \times \frac{2,78^2}{2 \times 9,81} = 0,4734 \text{ m} $

Pertes de charge linéaires totales:  

$\boxed{\Delta H_{\text{Lineaires}} = 0,8034 \text{ m}}$

  1. Calcul des pertes de charge singulières :
  • Sortie du réservoir :  $\Delta H_{K1} = 0,5 \times \frac{0,69^2}{2 \times 9,81} = 0,0121 \text{ m} $
  • Vanne : $\Delta H_{K2} = 0,2 \times \frac{0,69^2}{2 \times 9,81} = 0,0048 \text{ m} $
  • Changement de section : $\Delta H_{K3} = 0,35 \times \frac{0,69^2}{2 \times 9,81} = 0,0085 \text{ m} $
  • Clapet : $\Delta H_{K4} = 0,3 \times \frac{2,78^2}{2 \times 9,81} = 0,1183 \text{ m} $
  • Rétrécissement: $\Delta H_{K5} = 0,1 \times \frac{11,13^2}{2 \times 9,81} = 0,6314 \text{ m}$

Pertes de charge singulières totales:

$\boxed{\Delta H_{\text{Singulieres}} = 0,7751\text{ m}}$

3. Calcul des pertes de charge totales :

$\boxed{\boxed{\Delta H_{\text{Total}} = \Delta H_{\text{Lineaires}} + \Delta H_{\text{singulières}} = 1,5785 \text{ m}}}$

Les pertes de charges totales dans le circuit sont de 1,5785 m.

Publications connexes

Retour en haut